ENERO

Puntos Extremos:  Máximos y Mínimos

1. Máximos y Mínimos Relativos

Punto de silla 

Un punto de silla es aquel punto donde f(x,y) presenta un Mr con respecto a una variable y un mr con respecto a la otra

Ejemplo

Criterio de la segunda derivada:

Para utilizar el criterio de la segunda derivada se debe seguir los siguientes pasos:

2.- Máximos y Mínimos Absolutos

Toda función diferenciable en una región cotada y cerrada alcanza su valor máximo (o mínimo), o en un punto estacionario o en un punto de la frontera de la región.

Para obtener los máximos y mínimos absolutos en una región se debe seguir el siguiente procedimiento:

1.- Identificar la región en R2 y R3 sobre la cual se desea identificar los puntos extremos.

2.- Se buscan los puntos extremos en los puntos estacionarios.

3.- Se buscan los puntos extremos en los puntos de la frontera.

4.- Si alguno de los puntos no pertenece a la región no se toma en cuenta para determinar los puntos extremos

Ejemplo

3. Máximos y Mínimos Condicionados

      Método de los Multiplicadores de Lagrange

Se denomina extremo condicionado de una función f(x,y) al máximo o mínimo de esta función alcanzado con la condición de que las variables independientes esten relacionadas entre sí mediante la ecuación

g (x,y) = 0       Ecuación de Enlace

Para hallar los extremos condicionados de f (x,y) con la condición de enlace g(x,y)=0, se forma la función de Lagrange

F ( x, y, λ ) = f ( x, y ) + λ [ g (x, y) ]

Donde λ es el multiplicador de Lagrange (Parámetro constante Indeterminado)

Ejemplo:

Integrales Multiples

1. Integrales sobre regiones Rectangulares

Ejemplo

2. Integrales sobre regiones más Generales

Ejemplo

3.- Transformación de Integrales Multiples

Coordenadas Polares

x = r cos( θ)               (x,y)->(r,θ)

y = t sen( θ)                  |J| = r

Coordenadas Cilíndricas

x = r cos( θ)             (x,y,z)->(r,θ,z)

y = t sen( θ)                  |J| = r

z = z 

Coordenadas Esféricas

x = ρsen(Φ)cos( θ)        (x,y,z)->(ρ,θ,Φ)

y = ρsen(Φ)sen( θ)             |J| = ρ^2 sen(Φ)

z = ρcos(Φ)

Ejemplo

4.- Centros de masa

Para determinar las coordenadas del centro de masa se utiliza las siguientes formulas:

Distribución de masa lineal

Distribución de masa superficial

Distribución de masa volumétrica

Ejemplo

5.- Momentos de Inercia



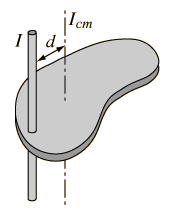
Ejemplo

Campos Vectoriales

En general un campo vectorial es una función cuyo dominio es un conjunto de puntos en R2 o bien en R3, y cuyo rango es un conjunto de vectores en V2 o en V3.

Definición

Sea D un conjunto en R2, una región plana. Un campo vectorial sobre R2 es una función F que asigna a cada punto (x,y) en D un vector bidimensional F(x,y).

Ejemplo:

Integral de Línea:

Una integral de linea es similar a una integral simple su diferencia radica que una integral simple integra una función en dos limites [a,b], en que esta lo hace a lo largo de una curva C. Acontinuación su definición:

Se considera de x=f(t) y y=f(t)

Masa y Centro de Masa

Con las Integrales de Línea también se puede obtener la Masa y Centro de Masa, respectivamente:

Integrales de Línea en el Espacio

Integrales de Línea una función de tres variables, en una curva en el espacio. (x=f(t), y=f(t) z=f(t)).

Ejemplo: